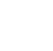Introduction
There are five basic methods used to calculate mass flux and/or mass discharge:
- transect methods: use individual monitoring points to integrate concentration and flow data (flow data are most commonly derived from aquifer tests but can be obtained from tracer tests)
- well capture/pump test methods: extract groundwater and measure the flow and mass discharge from the wells
- passive flux meters: estimate mass flux directly in wells
- transects based on isocontours
- solute transport models
Mass flux and/or mass discharge estimates are used to develop better CSMs (see Section 3.1), evaluate contaminant impact on downgradient receptors such as water supply wells or surface water (see Section 3.2), select and design remedies (see Section 3.3), determine the effectiveness of remediation projects (see Section 3.4), monitor compliance (see Section 3.5), and prioritize sites (see Section 3.6). Understanding the methods available for measuring and estimating mass flux and their relative strengths and limitations is important to making the best use of the information.
The following sections provide descriptions of these methods, a general comparison, and a discussion of the accuracy requirements for mass flux or mass discharge calculations. The technical backgrounds, strengths, and limitations of methods to calculate estimates of mass flux or mass discharge from the measured data and model simulations, and sources of uncertainty in the estimates are also presented.
4.1 Transect Methods
TM, the oldest and most common method, uses estimates of groundwater contaminant concentration and groundwater velocity at a series of monitoring points across a plume (Figure 4-1). TM has several variations with regard to the data collected and the methods used. TM is described by Nichols and Roth (2004) as follows:
[The transect method] relies on groundwater samples from single- or multi-level monitoring well data interpolated along a transect across the plume, perpendicular to groundwater flow. A vertical cross-section across the transect is divided into any number of sub-areas, each representing a discrete area of uniform concentration and groundwater flow discharge. The total mass flux is simply the sum of the fluxes from each of these subareas.
It should be noted the authors use the term “total mass flux” instead of “mass discharge.”
The transect is a control plane across the plume, perpendicular to the groundwater flow direction. Monitoring points (either temporary or permanent) within the control plane are sampled for contaminant concentration. Specific discharge of groundwater (also called Darcy velocity) through the control plane is also measured to provide flow data.
Theoretically the transect should be perpendicular to the actual flow vector so that at sites with vertical flow the transect would be not exactly vertical, but at an angle. At most sites, however, the horizontal flow component is significantly larger than the vertical flow component, and the error introduced by having an exactly vertical transect is likely to be small. Before installing a vertical transect, the vertical flow component should be estimated and compared to the horizontal flow component, and if there is a significant vertical flow, the transect may need to be redesigned or the flow calculation needs to account for only horizontal flow.
Some key insights on the type of monitoring well network were presented by Einarson and Mackay (2001):
- Single-screened wells may be useful if the vertical extent of the plume is limited or if the aquifer media (and groundwater flow) is relatively homogeneous.
- It is preferable to use transects of multilevel monitoring wells.
- If possible, the transect should be perpendicular to groundwater flow lines. If the flow lines are not parallel, the transect would (ideally) be curvilinear.
- To ensure all the mass discharge is captured, sampling points should extend a sufficient distance (both horizontally and vertically) so that the entire plume is bounded by nondetect points.
4.1.1 Steps to Apply the Transect Method
The following steps are typically used for estimating mass flux when using TM (Farhat, Newell, and Nichols 2006; Einarson and Mackay 2001):
Step 1. Characterize plume concentrations. For each selected plume transect, sufficient groundwater sampling points are needed to define the following:
- The full width and thickness of the plume (unless just a subsection of the plume is to be evaluated).
- The distribution of contaminant concentrations within the plume. Either single-level (typically wells that are fully screened across the plume) or multilevel groundwater monitoring points may be used for this purpose. Multilevel monitoring points provide a more detailed two-dimensional characterization of contaminant concentrations in groundwater. Nonetheless, single-level groundwater monitoring networks, while not providing a detailed picture of the vertical distribution of mass flux, are still used extensively to generate mass discharge estimates. For transects where single-level wells are not fully screened across the plume, users can either note that the calculated mass discharge is less than the actual mass discharge or do Step 4 (below) with a transect that includes extrapolated concentrations that extend to the estimated edge of the plumes. For example of this second option, if there is a transect with single-level wells that do not extend fully to an aquitard a short distance below the screened interval, one can extend the transect all the way to the aquitard if there is some basis for assuming the plume is located in this interval. Software tools such as the Mass Flux Toolkit (Farhat, Newell, Nichols 2006 and described below) can help users with this type of extrapolation.
Step 2. Characterize groundwater flow. To characterize the specific discharge of water or Darcy velocity (q) across each plume transect, representative measurements are required for both the hydraulic flow gradient (i) and the hydraulic conductivity (K) of the flow system (where q = K • i). Please note that heterogeneous conditions make collection of representative data more difficult (see Section 2.4.2). The groundwater flow direction and hydraulic gradient for each segment of a transect line can be determined from a potentiometric surface contour map based on static water level measurements at available sampling points. Representative measurements of the hydraulic conductivity of the groundwater-bearing unit should be obtained at one or more locations, using an appropriate method (e.g., pumping tests, slug tests, PFMs, borehole dilution (BHD) tests, tracer tests, or other techniques).
Step 3. Select plume transects. Transects should be located to define the distribution and concentrations of contaminants and specific discharge, as defined in Steps 1 and 2 above. Whether using multilevel or single-screen monitoring wells, the transect is a plane extending across the full width and depth of the plume, perpendicular to the direction of groundwater flow (Figure 4-2).
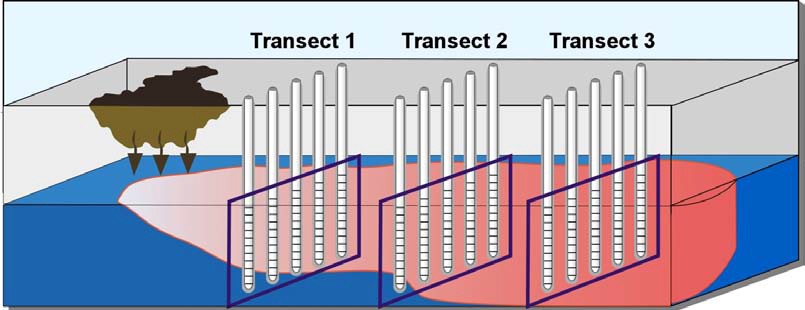
Figure 4-2. Example of multiple transects intercepting an MtBE plume.(Adapted from Einarson and Mackay 2001.)
Step 4. Apply interpolation method. At some sites, there will be a high-density array of concentration and groundwater flow data to support the mass flux calculations. At sites with less data, interpolation can fill gaps or smooth available concentration and/or flow data. There are several methods that can be used, including kriging, nearest neighbor, and Theissen polygons.
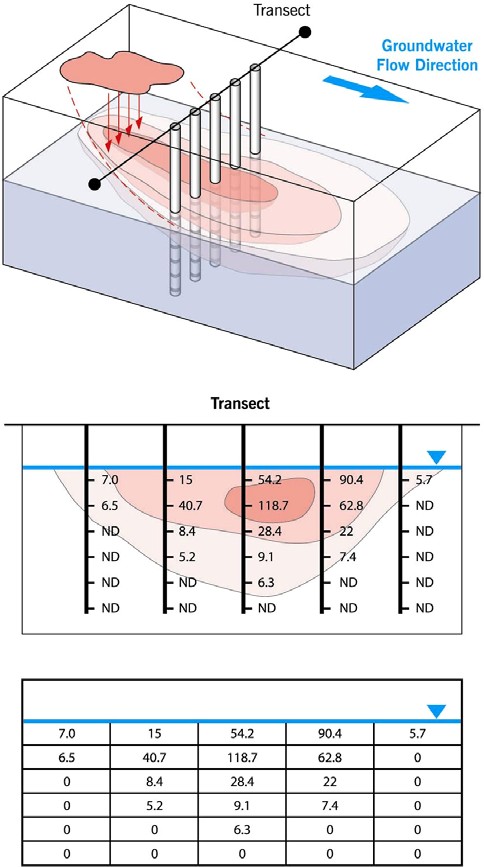
For the Theissen polygon method, one of the most commonly used techniques, each transect is divided into subareas (rectangles or polygons). Using the transect method, monitoring points are located directly on the transect to construct transect polygons. The dividing line between subareas is typically halfway between measurement points. For ease of calculation, the polygons should be reduced to rectangles if the monitoring points are uniformly spaced vertically; if the monitoring points are not uniformly spaced, then polygons are required (Figures 4-2 through 4-4 are examples of multiple vertical transects).
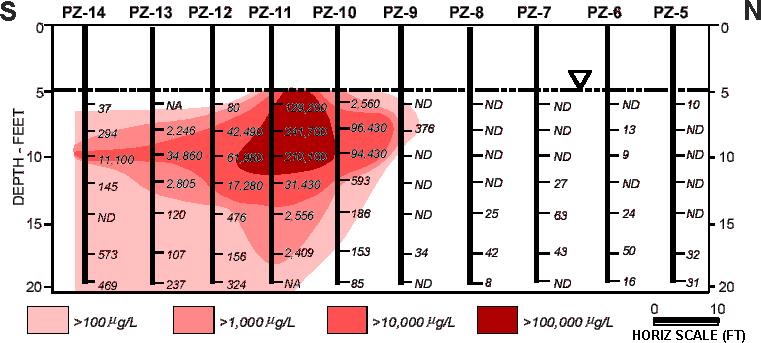
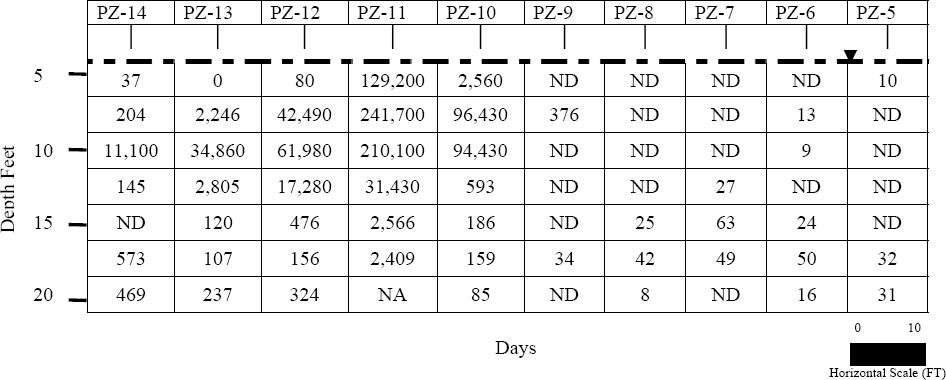
Figure 4-4 Transect 1 from Figures 4-2 and 4-3, which has been divided into polygons (rectangles). The polygons were created by drawing horizontal lines halfway between sampling points along each piezometer and the vertical lines halfway between each piezometer. The MtBE concentration (μg/L) is listed in the center of each polygon. (Einarson and Mackay 2001).
There are no accepted rules of thumb or general guidelines on what constitutes an appropriate sample density. Sections 2.5, 4.1.3, and 4.8 present research results and current knowledge related to the design of a mass flux/discharge system and the potential uncertainty associated with the results.
Kriging typically involves using a computer program to interpolate between data points (e.g., Isaaks and Srivastava 1989, Kitanidis and Shen 1996). The SURFER and Groundwater Modeling Software (GMS) software programs both include kriging algorithms. The nearest-neighbor algorithm is a simple interpolation technique where one simply selects the value of the nearest point, and does not consider the values of other neighboring points relative to that unknown point, yielding a piecewise-constant interpolation.
Step 5. Calculate mass discharge through the transect. The total contaminant mass discharge through the transect is calculated by summing the contributions from each of n polygons (rectangles in this case) as follows (as modified from Farhat, Newell, and Nichols 2006; see Table 4.1):
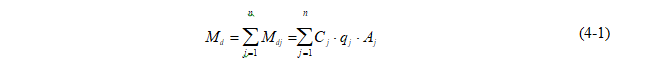
where
Md = mass discharge, M/t (e.g., g/d)
Mdj = portion of total transect mass discharge through polygon j, M/t (e.g., g/d)
Cj = concentration of constituent at polygon j in transect, M/L3 (e.g., mg/L or g/m3)
qj = specific discharge (also called Darcy velocity) through polygon j, L/t (e.g., m/d)
Aj = flow area through polygon j, L2 (e.g., length2 or m2)
qj can be calculated using eq. 4-2:
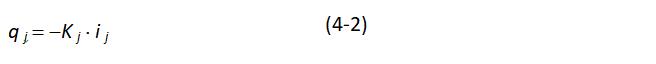
where
Kj = hydraulic conductivity at polygon j, L/t (e.g., cm/sec)
ij = hydraulic gradient at polygon j, L/L (e.g., cm/cm)
For example, in Figure 4.4, the portion of the total mass discharge from one of the polygons in the example above (in this case the polygon associated with the top reading for the PZ-11 piezometer), the calculation would be as follows (from Einarson and Mackay 2001):
Cj = 129,200 µg/L (129.2 mg/L) cis-DCE
Aj = 1.67 ft × 10 ft = 16.7 ft2 (0.52 m × 3.04 m = 1.55 m2) (the first 5 ft are divided into three rectangles so that the vertical distance for the top polygon is 1.67 ft)
q j = –K j × i j = 6.5 × 10^-3 cm/sec • –0.0029 ft/ft = 1.88 × 10^-5 cm/sec = 1.62 × 10^-2 m/d
(K was the average of several hydraulic conductivity measurements across this particular transect, and i was a measured hydraulic gradient through the transect
(example of Variation 1, see Section 4.1.3) (Einarson and Mackay 2001)
Mdj = Cj qj Aj
Mdj = 3.27 g/d (this is the mass flux from polygon [PZ-11, 5–6.67 ft] (Note: 1000 L per m3)
To calculate the mass discharge through the entire transect, this calculation is repeated for each polygon, and the results summed. The final units are in terms of mass per time, most commonly milligrams or grams per day or kilograms per year. In the example shown above, the mass discharge from all polygons is 31.0 g/d.
Table 4-1. Transect method summary (Adapted from Newell, Connor, and Rowan 2003.)

The Groundwater Remediation Strategies Tool (Newell, Connor, and Rowan 2003) and the Mass Flux Toolkit (Farhat, Newell, and Nichols 2006) are useful for completing mass discharge estimates.
4.1.2 Key Points Regarding the Transect Method
Some of the key considerations related to application of the transect method are summarized below.
- Sufficient data density is important. Contaminant plumes and groundwater flow fields are heterogeneous, where concentrations and specific discharge can vary by an order of magnitude (or more) over a few meters or less transverse to groundwater flow. Mass flux or mass discharge projects that sample more of the area of the transect (either by a large number of points or long screens that average concentrations) will be more likely to capture the high mass flux zones. When applying the transect method, practitioners must balance the need for accuracy with sampling density. For example, evaluation of the hydraulic conductivity of each polygon will improve the mass flux and discharge estimates concurrently with the collection of more discrete groundwater samples. Sections 2.5, 4.1.3, and 4.8 present research results and current knowledge related to the design of a mass flux/discharge system and the potential uncertainty associated with the results.
- Porosity is not used for mass flux/mass discharge calculations using the standard TM. Mass flux is determined by multiplying the specific discharge of a polygon (also called the Darcy velocity, in units of length divided by time) by the area of the polygon and the concentration in the polygon. Porosity is used for calculating seepage velocity (or average linear velocity), which represents the average rate at which the water moves between two points and is not applicable to mass flux or mass discharge calculations using the standard TM.
- Retardation (via the use of a retardation factor) is not a term in the equation to calculate mass flux. While important for solute transport and PFM calculations, retardation is not relevant to mass flux/discharge calculations because mass discharge/flux are based on the specific discharge that contains a contaminant. The geochemical system in each polygon is assumed to already be at steady state with respect to adsorptive processes.
- Mass flux can be calculated for any dissolved constituent. Metals, chlorinated organics, MtBE, inorganic ions—all can be evaluated using the mass flux methodology as long as the concentration data represent dissolved constituents migrating in flowing groundwater. The key concept is that contaminants are migrating in flowing groundwater and there is a measurement system (e.g., transect point, well capture, etc.) that samples the flowing groundwater.
However, if a large fraction of the contaminant mass is sorbed to suspended solids in the groundwater samples, then the mass flux calculations may be incorrect. For example, if unfiltered samples from an undeveloped well in a fine-grained unit are collected and if these samples have high concentrations of suspended solids with metals or organics sorbed to their surfaces, then the transport of these metals or organics will be overestimated (unless the groundwater is actually transporting the suspended solids). This problem can be avoided or minimized with properly developed wells, low-flow sampling techniques, passive sampling methods, or filtering samples. In most cases, however, properly collected groundwater samples are not highly turbid and therefore can be used for mass flux calculations. Cases where filtering might result in inaccurate results are cases where facilitated transport via colloids (e.g., plutonium) is an important transport process. (Note: The issue of filtering groundwater samples is complex and controversial. For more information see Matanoski and Murarka 1997, Luftig 2003, and Indiana DEM 2005).
4.1.3 Sampling Methods
Mass flux measurements can be performed using monitoring wells or temporary monitoring points installed with direct-push devices. Monitoring wells typically have longer screens (1.5 m or longer) that provide a flow-weighted concentration for that screened interval (if pumped at a high enough rate). Direct-push data will have shorter screened intervals (a few centimeters) but more sample points vertically. Various types of direct-push sampling devices (e.g., the BAT Sampler, ConeSipper, etc.) afford users very controlled and spatially distinct sampling and characterization opportunities. These devices can be deployed with many types of rigs. Furthermore, it is possible to collect complementary data and samples for the calculation of mass flux estimates during a single mobilization.
Mass discharge represents the overall mass passing through the control plane over a given period of time. The mass flux literature indicates that very dense vertical sampling (i.e., the short screen case) is needed if the goal is to detect concentration hot spots (e.g., Guilbeault, Parker, and Cherry 2005) or to know how mass flux (mass per area per time) is distributed across the control plane to optimize a remediation project targeting hot zones. If calculating mass discharge is the goal (for example, to quantify impact to a well or stream), either many points with short screens or a few wells with longer screens can be used. There are conflicting views about the use of long (≥10 ft) well screens for mass discharge estimates. In theory, a long well screen (if pumped hard enough) will provide a flow-weighted average concentration from that location and can be a cost-effective method to sample a large part of the aquifer. On the other hand, some researchers and practitioners feel that long well screens are not preferred for mass discharge monitoring without detailed site characterization (dense vertical aquifer sampling) that has demonstrated that the data from long-screened wells are representative of the vertical distribution of contaminants. The groundwater community is currently evaluating these complex issues.
At most sites, existing monitoring well networks are not designed to fully capture the mass flux through a particular transect. Instead, wells in such networks were designed to delineate plume boundaries, establish centerline plume concentrations, and provide estimates of source concentrations. (There are indirect methods that use conventional monitoring well network data to estimate mass flux, as described in Section 4-4.)
At some sites, the flow field is evaluated at a different resolution than the concentration field. For example, transects typically have multiple concentration measurement points (e.g., 70 monitoring points in the example shown in Figure 4-4). However, the number of aquifer testing points is more variable. At some sites, individual aquifer tests may be performed at each polygon, so the calculation of the polygon mass flux (Step 5 from Section 4.1.1) will have an individual concentration term (Ci) and individual hydraulic conductivity term (Ki). However, it is rare to have individual hydraulic gradient terms for each point, so a site-wide gradient is often used. Table 4-2 presents the most common variations of the transect method based on data density.
Table 4-2. Common variations of the transect method
| Variation | Concentration values (Cw) | Hydraulic conductivity values (K) | Hydraulic gradient values (i) |
| 1 | One per polygon | One per polygon | One for entire transect |
| 2 | One per polygon | Several for transect | One for entire transect |
| 3 | One per polygon | One for entire transect | One for entire transect |
At the current time, most examples of Variation 1 are from research sites; most examples of mass flux/mass discharge applications for site management purposes are based on Variations 2 and 3, though there is some disagreement among groundwater professionals who use the transect method regarding the accuracy of these methods. For example, Guilbeault, Parker, and Cherry (2005) state, “This assumption of homogenous hydraulic conductivity in sand aquifers is commonly used in calculations of plume mass-discharge (Semprini et al. 1995, Wilson et al. 2000).” In addition, several key research papers (e.g., Guilbeault Parker, and Cherry 2005; Nichols and Roth 2004; Einarson and McKay 2001) used Variation 3 to calculate mass discharge. Brooks et al. (2008) used Variation 3 of the TM to compute mass discharge values at two sites and compared these results against the PFM and a pumping test method (see Sections 4.2.5 and 4.3.2). In this case, hydraulic conductivity values from groundwater models were used to estimate a transect-wide hydraulic conductivity value. The authors commented on the use of transect-wide estimates of hydraulic properties as follows:
As employed here, TM results may have been impacted by uncertainty associated with homogeneity assumptions in order to use (a transect-wide) K and (a transect-wide) i to calculate (a transect-wide) q. The appropriateness of using (a transect-wide) K and (a transect-wide) i estimates to complete the TM approach given the spatial variability of PFM results may be questioned; however, hydraulic conductivity values based on pumping tests or slug tests completed at one or a few locations across a site and site-wide estimates of hydraulic gradient are routinely used in typical site characterization approaches.
Li and Abriola (2009) evaluated different sampling strategies for estimating mass discharge and concluded, “for highly heterogeneous permeability fields, the uncertainty from the permeability field may contribute significantly to the uncertainty of mass discharge; therefore, characterization of the permeability field may be important and statistics from the permeability field may need to be incorporated in the sampling algorithm.” Basu et al. (2006) used both Variations 1 and 3 to estimate mass discharge at a TCE site in the Midwest. PFMs were used to estimate concentrations and specific discharge at multiple points across a transect. These values were then used to estimate a mass discharge of the 365 g/d using Variation 1 and 414 g/d using Variation 3 (13% difference in mass discharge). The authors commented that Variation 1 “yielded a better estimate” of the source strength than Variation 3.
Kübert and Finkel (2005) compared several methods, including Variations 1 and 3, by constructing a hypothetical plume and applying Monte Carlo techniques to evaluate error. Comparing Variation 3 (their Method D) with Variation 1 (their method C) revealed that both methods show the same performance for low- to moderate-conductivity variances (aquifer heterogeneity) with “no significant difference” in the error of the two variations. For larger variances in hydraulic conductivity in the hypothetical plume, the result of the comparison depends on the sampling grid resolution: while Variation 3 “performs better for coarse resolutions (horizontally and/or vertically),” Variation 1 “yields a higher accuracy if sampling wells or levels are close.” However, if the sampling grid is inappropriately designed, Variation 1 may lead to a severe misinterpretation due to inaccurate well-specific hydraulic conductivity values. Kübert and Finkel (2005) also concluded that the use of well-specific hydraulic gradient values did not show any significant reduction in estimation errors.
In summary, Variation 1 is likely to provide more accurate mass flux or mass discharge estimates than Variation 2, and Variation 2 will likely be more accurate than Variation 3. However, many (or perhaps most) of the mass flux or mass discharge calculations performed using the transect method now (i.e., in the 2010 time frame) are probably calculated using Variation 3. It is difficult to determine the accuracy of different mass flux/discharge calculation methods. Section 4.8 provides a discussion of uncertainty issues related to mass flux/discharge in general.
4.1.4 Data Analysis Methods
When calculating mass flux/discharge from data-rich transects, the user likely will determine the subarea or polygon boundaries as follows:
- drawing rectangles or polygons around the concentration monitoring points (The polygons are formed by connecting lines at the halfway point between each sampling point on the transect.)
- truncating the subareas in areas where the plume is no longer present (This could be where non-detect values are measured or the edge of the plume is anticipated to be.)
- accounting for hydrogeologic boundaries such as the top of the water table, a confining unit at the top, and/or an aquitard at the bottom of the water-bearing unit
- accounting for cases where there are different sampling densities of concentration, hydraulic conductivity, and hydraulic gradient data (for example, a transect with 30 concentration estimates, 5 hydraulic conductivity estimates, and a uniform hydraulic gradient estimate across the transect)
The first method to determine mass flux/mass discharge is to set up the array of subareas or polygons. There are several computation techniques, with the most common described below. The first method is to compute the mass discharge for each polygon separately. The calculations can be quite labor-intensive as one progresses across the aquifer.
A second approach is to put the data into a spreadsheets, with one array showing the concentration data, another array showing hydraulic conductivity data, and a third array showing hydraulic gradient data. Cells in each array represent subareas, and the data for each subarea on each of the three arrays are used to calculate the subarea mass flux in a fourth array (after making the appropriate conversions).
A third approach is to interpolate the distribution of the contaminant in the vertical plane using software contouring or kriging packages. The pros and cons of using computer software to contour groundwater data are well known to groundwater professionals. While computer contouring methods do provide considerable labor-saving advantages, particularly for large datasets, one researcher (Siegel 2008) has stated that hydrogeologists should “contour using your head, not your computer,” and has listed this rule as one of the 10 “fundamental principles” of hydrogeology. If computer contouring is used, it should be carefully checked to make certain that boundary conditions and internal points are honored and that the final output is a reasonable representation of the contaminant distribution.
A fourth approach is calculate mass flux using specialized software, such as the Mass Flux Toolkit program (Farhat, Newell, and Nichols 2006), a free downloadable software tool developed as part of the Department of Defense Environmental Security Technology Certification Program (ESTCP) research program. With this tool, users enter concentration data in terms of coordinates and type of monitoring point (single point or screened interval from monitoring wells). Next hydraulic conductivity data are entered or imported from electronic datasets (either as multiple points or a single site-wide estimate), followed by hydraulic gradient data. Figure 4-5 shows the input screen for the Mass Flux Toolkit. Users can then select the type and resolution of the subarea grid. Many times the available data do not fill an entire grid of subareas, so users select one of several ways to interpolate the “in-between” data, including nearest neighbor, linear interpolation, or log interpolation (recommended by some practitioners as the best method) or enter their own estimated values. Figure 4-6 shows the results screen for a transect calculation involving MtBE.
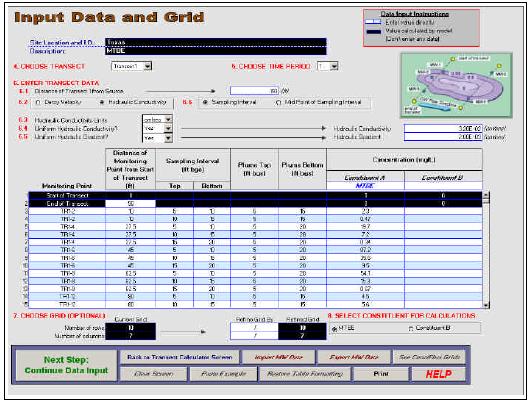
Figure 4-5. Input screen for Mass Flux Toolkit. (Farhat, Newell, and Nichols 2006)
More than one transect can be calculated to show how mass flux changes as one moves farther downgradient from the source zone, and transect data over time can be entered to evaluate temporal changes in mass flux. A detailed case study is provided as Example 1 in the Mass Flux Toolkit User’s Manual.
4.1.5 Uncertainty Associated with the Transect Method
Mass discharge estimates are based on integrating flow and concentration data, both of which have uncertainty; therefore, the overall mass discharge value itself will have some uncertainty. Nichols and Roth (2004) summarized the uncertainty in transect-based mass flux estimates as follows:
Although the transect method allows for an improved understanding of the concentration distribution across a plume and is easy to calculate, the underlying assumptions (e.g., that the monitoring well transect adequately describes the plume) and data required may impart an unknown degree of uncertainty in the resulting mass-flux estimate. Reducing uncertainty with this method may require that many samples be taken in space and over time, with potentially higher analytical cost.
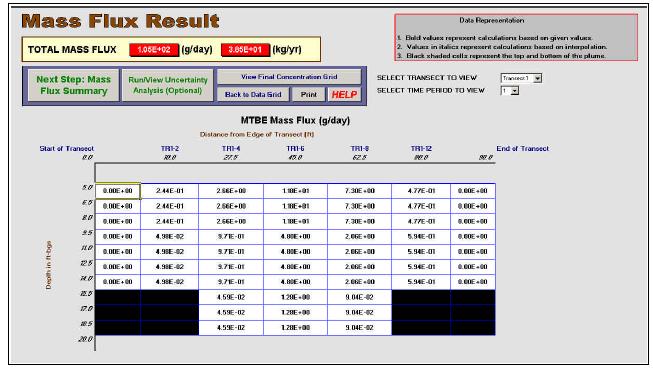
Figure 4-6. Results screen for Mass Flux Toolkit. (Farhat, Newell, and Nichols 2006)
Einarson and Mackay (2001) concluded as follows:
There are, of course, uncertainties associated with the calculation of contaminant Md (mass discharge) using data collected from sampling transects. Uncertainties are associated with the density of the sampling grid, methods used to integrate the mass traversing the transect (techniques for integrating the contaminant mass typically include numerical kriging routines and Theissen polygons), and estimation of the groundwater specific discharge within each hydrostratigraphic unit. It should be noted that the accuracy of the Md estimate is, in general, likely to improve with the number of monitoring points in the sampling transect.
(Note: Einarson and Mackay use and describe the calculation of mass discharge [units of mass per time flowing through a vertical transect] but interpret Md as mass flux, which is actually units of mass per area per time.)
The Mass Flux Toolkit provides quantitative examples of uncertainty. For example, Fraser, McLaren, and Barker (2005) evaluated mass flux vs. sampling density for a naphthalene plume at the Borden research aquifer:
When the sampling grid density was reduced from 1.7 points per meter squared to 0.7 points per meter squared, the range (as a standard deviation) in mass discharge increased to more than 50%. Guilbeault et al. (2005) showed that 75% of the mass flux occurred within 5% to 10% of the transect cross section area for three plumes in Ontario, New Hampshire and Florida, and that a spacing no larger than 15 to 30 cm was needed at some locations to identify high concentration zones. However, mass flux calculations using a relatively sparse sampling network (<10 sampling points) for two transects showed similar total mass flux estimates (Nichols et al. 2005).
The Mass Flux Toolkit identified three main sources of uncertainty associated with the transect method:
- Type 1. Uncertainty in the actual concentration, hydraulic conductivity, and gradient measurements. Uncertainty in the water quality data (concentration) is due to variability over time and space. Temporal uncertainty can be estimated by evaluating temporal trends over time and evaluating the amount of “time-independent” data variability (basically the scatter observed above and below a trend line). Therefore, a mass flux/discharge estimate derived using point concentrations from a single sample event will have uncertainty due to time- independent variability (for more information on time-independent variability in point concentration measurements, see McHugh, Liu, and Newell 2010). Spatial uncertainty relates to whether the measurement grid was able to capture the variability in groundwater concentrations in the transect. Groundwater practitioners can estimate the accuracy of the hydrologic measurements (hydraulic conductivity and hydraulic gradient) that are being used for the mass flux calculation. At most sites, the use of a single value for hydraulic conductivity and hydraulic gradient will produce uncertainty. Remediation Hydraulics (Payne, Quinnan, and Potter 2008) provides a detailed evaluation of the variation in hydraulic conductivity at the plume-level scale.
- Type 2. Uncertainty in the interpolation scheme. Different interpolation schemes will result in different mass flux estimates. Some interpolation schemes, such as kriging, provide local estimates of uncertainty.
- Type 3. Uncertainty associated with unmeasured values. The uncertainty associated with areas of high mass flux that may be missed by the monitoring scheme is difficult to assess.
To help users understand and manage this uncertainty, the Mass Flux Toolkit includes an uncertainty module that uses a Monte Carlo approach (a class of computational algorithms that rely on repeated random sampling to compute their results) to analyze the Type 1 uncertainty in the actual concentration, hydraulic conductivity, and gradient measurements. With this tool, groundwater practitioners can estimate the accuracy of the hydrologic measurements used for the mass flux calculation. Instead of a single value, users input a probability distributions of all of the key input variables, such as contaminant concentration, hydraulic conductivity, and gradient. The Monte Carlo algorithm calculates thousands or tens of thousands of “realizations” and performs statistics to describe the potential for different output results. While a relatively simple statistical method, this approach requires that the users know or estimate the probability distributions of the key input variables. In addition, it is not calibrated to actual measurements and assumes independency among input variables, which may cause overestimation of the mass flux uncertainty.
Another uncertainty option is a geostatistical approach that quantifies mass discharge and the associated uncertainty using geostatistical stochastic simulation (Li, Goovaerts, and Abriola 2007). This approach evaluates the Type 2 and Type 3 uncertainty and provides a range of possible mass discharge values with the probability of occurrence. This approach essentially generates many equally probable mass flux realizations for the transect, which are all representative of the sample data. The possible mass discharge values are then calculated from these mass flux realizations. This approach is similar to the Monte Carlo approach, but it does not require prior information about input variables; it is conditional to the data and considers the correlation between input variables.
4.1.6 Transect Method Using Advanced Piezocone/Membrane Interface Probe/Confirmation Method
A modification of the transect method developed by Kram et al. (2008) employs the high- resolution piezocone (HRP), a MIP, and confirmation analyses to estimate plume characteristics, including mass flux distribution estimates in two and three dimensions (transects in any orientation: vertical, horizontal, or at an angle). Key procedural elements and technologies are briefly discussed below.
A piezocone (American Society of Testing and Materials [ASTM] D5778 and D6067) is a sensor probe consisting of a porous element connected to a customized transducer that converts pore water pressure to water level. A high-resolution piezocone (U.S. Patents 6,208,940 and 6,236,941) is a push sensor probe capable of generating highly resolved hydraulic head values (±1 inch of water level) while simultaneously collecting critical soil type information. The porous element is filled with viscous oil that is in contact with the transducer, which is located inside the probe housing. As the probe is advanced through the soil, water pressures are transferred through the oil-filled porous element directly to the transducer. The signal is recorded and converted to hydraulic head estimations through correlations between recorded signal and hydrostatic pressure. Since the environment is disturbed when the probe is advanced, dissipation of the pressure while the probe is held in place yields critical information related to hydraulic conductivity. The piezocone is also capable of generating soil type estimates based on measurements of vertical resistance to force and sleeve friction or on pore pressure and vertical resistance to force.
Figure 4-7 displays one available WinOCPT version of the HRP output for a single push with five dissipation tests. From the left are columns representing soil type classification, hydraulic conductivity (based on a Robertson and Campanella [1989] lookup chart), hydraulic conductivity at specific depths (based on Parez and Fauriel [1988] pressure dissipation relationships), and effective porosity estimates (based on soil type lookup chart). Depths are listed along the y axes. The dissipation curves for specific depths where tests were conducted are displayed along the lower right portion of the graphic. Final pressures and hydraulic conductivity values are derived from this dissipation test summary. The hydraulic pressure profile is presented in the upper-right graph, along with calculated water depth below surface and corrected water table depth (relative to sea level). All hydraulic data becomes available for additional processing via the GMS platform.
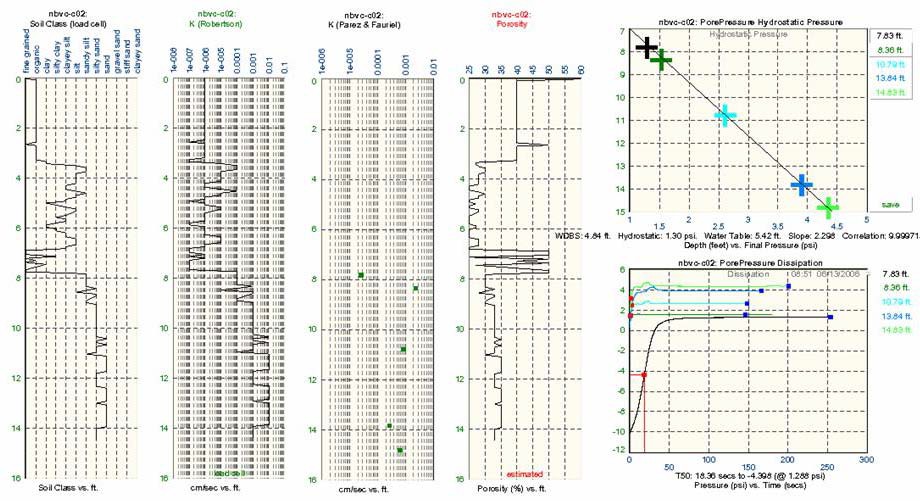
Figure 4-7. High-resolution piezocone output example for a single push. Moving left to right, panels of data show soil type versus depth, hydraulic conductivity versus depth (based on the Robertson and Campanella [1989] soil type conversion), hydraulic conductivity versus depth (based on the Parez and Fauriel [1988] relationships), effective porosity, pressure dissipation tests for specific depths, and head versus depth. Dissipation tests are used to determine K and head values for specific test depths. (Kram et al. 2008)
The MIP is a semiquantitative tool for the characterization of contaminant concentrations. It incorporates a thin polymer film supported by a stainless screen. The film is a permeable membrane through which volatile contaminants and aquifer constituents migrate. It is placed in a heated block attached to the probe and heated to approximately 100–120ºC. A carrier gas sweeps the zone where volatile constituents that have passed through the film have collected and brings them to the surface for rapid analysis via gas chromatography or ion trap mass spectrometry. A new heated trunkline MIP system has recently been commercialized to increase the accuracy of this screening tool. However, confirmation samples are always recommended and, in the opinion of some, necessary for mass flux/discharge calculation.
In addition, the MIP samples the entire matrix, including NAPL, dissolved phase, and sorbed phase. Therefore, using MIP data for mass discharge calculation may bias the results as mass flux/discharge are defined as aqueous-phase concentrations only. Nevertheless, other concentration measurement methods can be used with the piezocone technique for mass discharge calculation.
The hydraulic data (from the HRP) can be combined with the contaminant distribution (e.g., from the MIP and confirmation data) using a calculation tool such as the GMS package. The end result is a distribution of mass flux across the transect. For this approach, GMS has been modified to allow practitioners to interpolate key parameters and then calculate both the groundwater velocity and mass flux distributions. Hydraulic conductivity interpolation options include conventional geostatistical approaches and coupled soil type and dissipation value constraints, as well as more complicated approaches such as the Markov Chain transitional probabilities techniques (an interpolation approach that is useful when articulating the geospatial relationship of facies and other similar types of deposits and characteristics).
A key requirement includes conversion of individual head values from the piezocone to a gradient field. This is accomplished using a finite-difference approach to solve for gradient at each grid node. At each node, colocated interpolated K and effective porosity values are merged with gradient to calculate seepage velocity; then this value is merged with colocated and interpolated concentration values resulting from the chemical concentration estimates. The net result is a three-dimensional flux distribution field. Transects of flux distributions can be generated using the visualization tools in GMS. A mass discharge value can be derived by integrating the flux distribution across the transect. This surface can represent a source control plane or any other transect (e.g., plume centerline) of interest.
Mass discharge can be estimated by integrating the mass flux values throughout the plane, which converts the individual flux values (in mass/area/time) to a time-stamped cumulative flux (or discharge value) in units of mass/time. Note that the existing version of the piezocone/ MIP/confirmation version uses seepage velocity to calculate mass flux, while the calculation of mass discharge through a transect using the definitions in this document would require the use of specific discharge (also called Darcy groundwater velocity) to calculate mass discharge. Future software iterations in development will enable modelers to use either relationship.
The GMS software package can be used to interpolate between measured transects (either at different places in the plume and/or at different times) to generate interpolated mass flux. Note that the uncertainty in the interpolated mass flux data is likely to be higher than the uncertainty in mass flux data generated from piezocone/MIP/confirmation measurements at actual transects. In practice, uncertainty can be reduced by collecting data from locations reflecting the highest levels of uncertainty (e.g., within and around the plume between transects intended to be used for long-term monitoring). An appropriate field sequence of data collection activities could be as follows: deployment of the semiquantitative MIP for plume delineation, use of a confirmation sample collection tool for dissolved-phase quantification and MIP value normalizations, then deployment of the HRP for detailed hydraulic assessment in discrete locations as a basis for remediation design and to establish long-term monitoring networks for remediation performance evaluation. Once a long-term monitoring network has been deployed, head and concentration values can be measured and processed using GMS to derive time-lapsed flux assessments. Pneumatic slug-testing of the installed monitoring points can be performed and compared to the hydraulic information originally provided by the piezocone.
Key limitations or issues to the method are as follows:
- The interpolation methods may not be robust between transects.
- The use of the MIPs may not accurately capture the mass flux in groundwater due to measurement of sorbed and NAPL phases (if present).
To date, the HRP method has not been directly compared to other more traditional flux and discharge characterization approaches included in this document. Kram et al. (2008) used a control approach composed of 39 customized small screen wells (e.g., 3/4-inch diameter with 6- inch prepacked screens) installed in 13 clusters, each composed of three wells set to three specific depth ranges within the anticipated solute travel pathway of the test domain. The test cell spanned 10 × 25 ft (in map view). Head and hydraulic conductivity measurements were performed in each well, then compared to the HRP readings from identical depths and offset by 1 ft in map view. While slight directional and velocity nuances associated with each data set were observed, the general gradient and head distributions displayed exceptional agreement within the well cluster domain. Hydraulic measurements from each data set (HRP and wells) were incorporated into flux models by simulating solute transport and concentration distributions over time based on the exported velocity fields resulting from each of the measurement data sets. Concentrations were incorporated into GMS flux renderings by combining the simulated concentration fields over time with velocity fields derived for each data set, with very good agreement (e.g., spatial, temporal, and via model efficiency metrics) between the well and HRP- derived iterations.
4.2 Well Capture/Pumping Test Methods
4.2.1 Well Capture Method
Nichols and Roth (2004) describe an alternative mass discharge method in which an extraction well fully captures a contaminant plume (Figure 4-8). By measuring the concentration and flow rate of the well, the mass discharge (in units of mass per time) can be calculated. This approach assumes that the well or well system fully captures the horizontal and vertical extent of the contaminant plume and that the well (or wells) is located far enough downgradient of the source that the pumping does not induce high discharge of contaminants from the source due to increased dissolution of source materials. This distance can be evaluated using the concept of drawdown cones, which can be evaluated using the Theis equation or a groundwater flow model. For permeable aquifers used for water supply, this distance is often relatively small. One advantage of this method is that the well is an effective tool to integrate flow and concentration so that even small concentration hot spots and high-transmissivity zones are captured by the well. The method has relatively few data requirements, but the test must achieve the following conditions:
(a) the pumping well should not increase the flow through the source zone (this might increase the dissolution rate and concentrations may or may not change), (b) pumping should be continued long enough so that relatively steady-state, and (c) complete or near-complete capture of the high-discharge portions of the plume must be confirmed using groundwater potentiometric surface data or tracers. The need for complete capture is a site-specific decision depending on the level of accuracy needed at a particular site. Performance monitoring data from most hydraulic capture systems will provide mass discharge data once flow rate and concentration data are multiplied using appropriate conversion factors.
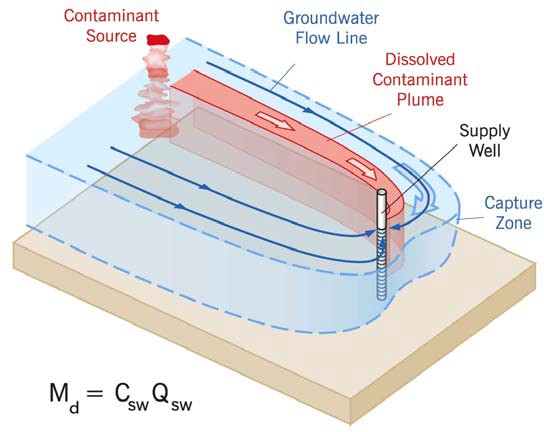
Md = mass discharge, Csw
= concentration from the supply well, Qsw = flow rate of the supply well. (Nichols and Roth 2004)
One of the most easily performed and least expensive estimates of mass discharge can be obtained from existing data from a pump-and-treat system, which inherently uses the well capture method (if the system captures the entire plume). Existing pump-and-treat systems, where both flow and concentration data are collected, are often ideal “monitoring systems” to determine mass discharge. Changes in the concentration over time can make the interpretation of test results more complicated. Unfortunately for some purposes, the spatial distribution of mass flux (in units of mass per time per area) is not revealed using this method unless multiple recovery wells are involved where individual headers can be sampled. This is the key disadvantage to the well capture method in that the site managers only get the single value, mass discharge in units of mass/time. Information about the structure of the plume, the location of high-discharge zones, etc. is not provided by this method.
Calculation Approach
In its simplest form, the following calculation is used to determine mass discharge from any pumping well that has captured a plume (modified from Nichols and Roth 2004):

where
Md = mass discharge in units of mass per time, M/t (e.g., g/d)
Csw = concentration of contaminant in the extracted well water, M/L3 (e.g., mg/volume)
Qsw = water flow (pumping) from the well, L3/t (e.g., volume/d)
If more than one well is used, the values are summed to determine the mass discharge.
4.2.2 Integral Pump Test
A more sophisticated well capture method, the IPT, was developed by researchers at the University of Tubingen in Germany (Holder et al. 1998; Schwarz et al. 1998; Ptak and Teutsch 2000; Teutsch et al. 2000; Bockelmann, Ptak, and Teutsch 2001). Using frequent concentration values measured in the discharge from a pumping well over the duration of a pump test, an analytical solution is then used to back-calculate the mass discharge (see Section 4.2.2.1) that would be required to produce the observed concentration vs. time data. The method assumes (a) steady-state conditions, (b) homogeneous or moderately heterogeneous conditions (i.e., conditions where the scale of local heterogeneities is much smaller than the investigation scale; the analytical solution derived for homogeneous and isotropic formations [Swartz et al. 1998; Bockelmann, Ptak, and Teutsch 2001] may not be accurate for highly heterogeneous aquifers), (c) the equation is practical only for radially symmetrical capture zones, and (d) negligible or linear contaminant concentration gradient within each capture well zone flow path. In more sophisticated analyses, numerical solute transport models are used to reconstruct mass flux patterns in a water-bearing unit at complex sites. Figure 4-9 shows a conceptual depiction of the time series approach.
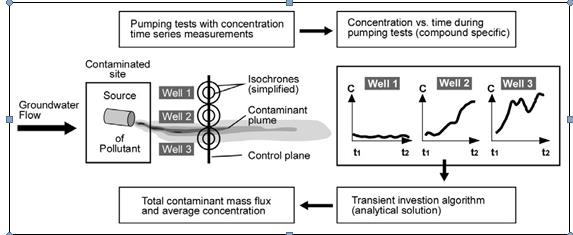
Figure 4-9. Process for estimating mass flux using integral pump test series data. (Bockelmann, Ptak, and Teutsch 2001)
More recently Bauer et al. (2004) and Bayer-Raich et al. (2006) have refined the IPT method to account for the combined effects of linear instantaneous sorption/retardation and multiple wells.
4.2.2.1 Integral Pump Test Advantages and Limitations
The advantages of the IPT method include the following:
- does not require interpolation of contaminant concentrations between subareas
- requires fewer wells (only pumping well[s] and enough monitoring wells to ensure that the entire plume has been captured)
- samples large quantities of plume water, which results in better flow and concentration data and improves integration results
- can be applied to existing plume containment systems
The limitations of the IPT method include the following:
- can generate large volumes of contaminated water, which must be managed
- pumping can change plume chemistry, such as by introduction of oxygen-rich water from clean zones
- can be difficult to determine whether plume is fully captured by the pumping well(s)
- if the pumping well is in the source zone, the dissolution rate may change compared to conditions prior to pumping
- no information on the spatial distribution of contamination parallel to groundwater flow
- difficulty in obtaining a unique solution
Calculation Approach
With the IPT, the concentration vs. time data from the pumping well(s) are combined with solute transport models to derive the upstream concentration field under natural-flow conditions to yield a mass discharge. The developers of the method have used both analytical and numerical solutions to derive a backwards-calculation approach where conditions in the aquifer and plume are reconstructed so that they result in the observed concentrations coming from the pumping well.
In the Bayer-Raich et al. (2006) methodology, the mass discharge along a multiple well IPT control plane is obtained from the following equations:
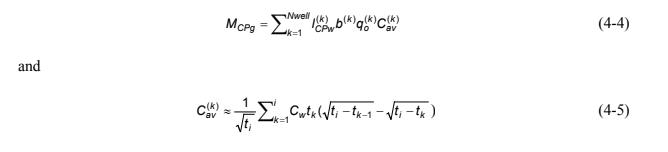
where


Note the analytical method is not able to uniquely predict the spatial distribution of concentration in the dimension perpendicular to flow. In other words, there could be several different concentration profiles (plume contours in the vertical transect) that could explain the signal generated by this type of pumping test. Therefore, there is some uncertainty in this method, and in some cases the final answer (average concentration) may not exactly match what is actually present in the field.
4.2.3 Modified Integral Pump Test
The modified integral pump test (MIPT) is a simple field method which can be used to estimate contaminant mass flux averaged over a large subsurface volume. The method is different from IPT in that it is used to measure the Darcy velocity directly (without separate measurements of hydraulic conductivity and hydraulic gradient) and avoids the need for complex data analysis.
The MIPT method assumes that the aquifer is confined, isotropic, and homogenous (i.e., the transmissivity, which is the hydraulic conductivity multiplied by the aquifer saturated thickness, is constant) with a uniform thickness (b) under steady-state and uniform flow conditions. Note that these are the same assumptions required to evaluate pump test data with the commonly applied Theis method and other aquifer test analysis methods. The Darcy velocity (q0) can be determined by measuring the head difference between pumping wells and monitoring wells, when the pumping wells are pumped at different flow rates. For an aquifer of thickness b and a transect perpendicular to groundwater flow, the head difference, Δh, between a pumping well at the origin and a downgradient monitoring well at distance, Δx, can be expressed by the following equation (Brooks et al. 2008, Goltz et al. 2009):

If the field measurements of Δh are plotted by the following function:
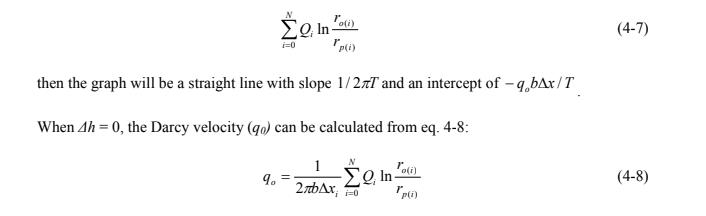
After the Darcy velocity is calculated, the mass flux can be determined by multiplying q0 by the contaminant concentration. The contaminant concentration estimates are made over time at the pumping well and averaged.
The MIPT can be considered an emerging method to calculate mass flux (Goltz et al. 2009). It has been applied at several field sites, including sites in Utah (Hill Air Force Base [AFB]), Washington (Ft. Lewis, as reported by Brooks et al. [2008]), the Borden Site in Canada, and a site in Jacksonville, Florida.
4.2.4 Tandem Circulating Wells
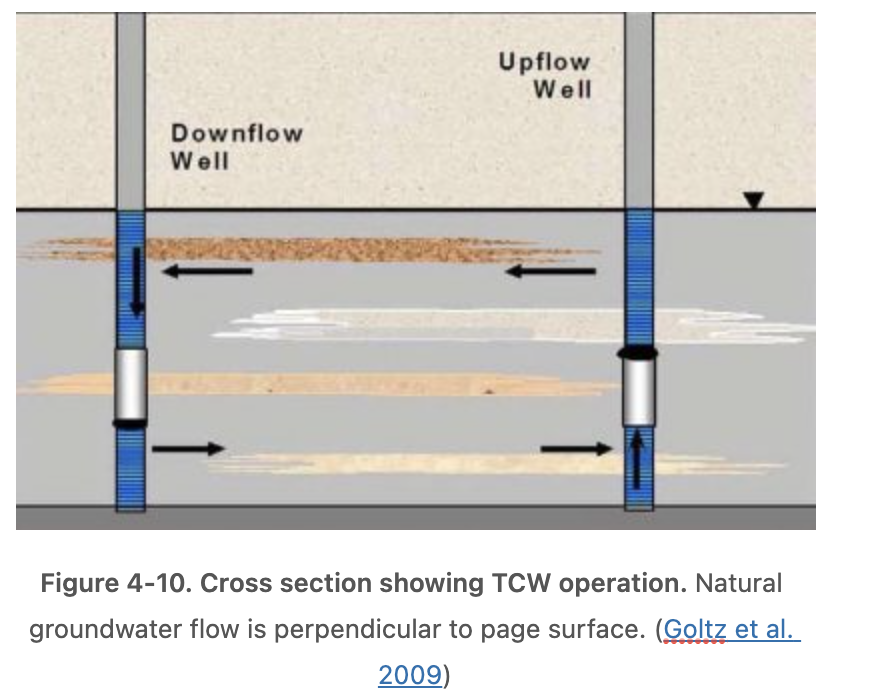
Another well pumping method to measure mass flux is the use of tandem circulating wells (TCWs), also called tandem recirculating wells (TRWs). This method should be considered as an experimental approach as it has not been applied in the field to calculate mass flux (Goltz et al. 2009). The method uses two dual-screened wells: one extracts water from a lower depth and pumps it upward to inject at a shallow depth; the second operates in the opposite direction. This arrangement results in the water circulating between the two wells without being brought to the surface (Figure 4-10).
For calculating the mass flux, the hydraulic gradient can be determined by measuring the pieziometric surface at the two wells (with the pumps turned off) and a third piezometer, located near the pumping well, to form a triangle of wells. Hydraulic conductivity is then measured by pumping the two wells and evaluating the resulting head data from the wells. Contaminantconcentration is measured by sampling the contaminated water as it flows through the wells. Mass discharge is then obtained by combining the gradient, hydraulic conductivity, and concentration data. The primary advantage of this method is that no wastewater is produced. One potential difficulty is that some regulatory agencies are hesitant to allow reinjection of contaminated groundwater into an aquifer, even if the aquifer is already contaminated and the groundwater is not pumped above grade (see USEPA 2000).
A modification of the TCW method is the addition of a tracer. This technique determines the fractional flow between the two wells by injecting and monitoring tracers at the two injection screens. The fractional flow is the fraction of water drawn into one well’s extraction screen that originated from the other well’s injection screen. Possible tracers include bromide, chloride, and nitrate, one injected into the upflow well and one into the downflow well. This method has not been applied at a field site as of mid-2010.
4.2.5 Comparison of Well Capture/Pump Test Methods to Transect Method
The MIPT has been compared to other mass discharge estimate methods at two sites (Brooks et al. 2008):
- Hill AFB
- pretreatment—MIPT: 76 g/d, TM: 78 g/d
- post-treatment—MIPT: 3.9 g/d, TM: 7.2 g/d
- Ft. Lewis
- pretreatment—MIPT: 466 g/d, TM: 599 g/d
- post-treatment—MIPT: 1.5 g/d, TM: 1.9 g/d
All transect method calculations were performed using Variation 3, where average hydraulic conductivity values are determined during previous characterization efforts. Both the Hill and Ft. Lewis transects comprised 10 wells with 5–21 vertical measurements per well.
The Hill AFB site overlooks the Weber Valley and is located on a terrace in an east-facing slope of an old floodplain formed by the Weber River. The shallow, unconfined, paleo-channel aquifer at the site occurs in heterogeneous alluvium (Brooks et al. 2008). The transect-wide average specific discharge (q) determined from PFM deployments was 2.5 ± 1.8 cm/d (spatial mean and standard deviation of all PFM measurements) for pretreatment conditions and 1.5 ± 0.7 cm/d under post-treatment conditions.
The Ft. Lewis site has a surficial, unconfined aquifer composed of the Vashon Recessional Outwash/Steilacoom gravel unit, consisting of loose, well-graded, sandy, cobbly gravel or gravelly sand. In the immediate vicinity of the site, this unit is underlain by Vashon Till, consisting of loose to dense silty, sandy gravel with some clay, which is considered to be a generally continuous intermediate aquitard (Brooks et al. 2008). Tracer depletion data from PFM deployments yielded a transect-wide average specific discharge (q) estimate of 27 ± 19 cm/d for pretreatment conditions and 16 ± 12 cm/d under post-treatment conditions.
The absolute accuracy of either method is not known. The relative differences between the two methods range from –46% to –3%, calculated by the equation (TM measurements – IPT measurements) ÷ TM measurements. The differences are relatively small considering the variability in groundwater flow and groundwater monitoring data and the overall range in mass discharge estimates, which has a factor of 200 or more.
4.2.6 Sensitivity/Uncertainty
IPTs also have uncertainties associated with flux calculations. Inevitably, one must extrapolate from the induced-flow measurements to the flux under natural flow conditions, and there may be errors inherent in such extrapolations. One source of error is pumping-induced changes in the natural flow regime in the area. Perhaps more importantly, pumping may draw water from less- transmissive zones or “dead-end” fractures or pores that do not normally contribute to the mass flux. Such waters can contain relatively high contaminant concentrations since they transmit little to no flow and therefore may be in equilibrium with near-solubility pore water concentrations in the surrounding matrix. However, regardless of contaminant concentrations, the energy required to draw water from low-transmissivity zones would be substantially greater than that required to draw a greater than nonpumping conditions volume of water from more transmissive zones. Therefore, the impact of contaminants in water from less-transmissive zones on the total mass would not be proportional to their percentage of the aquifer volume.
There are other potential sources of error in pumping tests. There is the potential for missing part of the plume, given the difficulties in finding and fully delineating source zones and in predicting capture zones. In addition, spatial information is sacrificed to some extent in pumping tests as opposed to discrete transect sampling. However, careful measurement of contaminant pulses during pumping can provide some information on the distances between flux pathways and the extraction well (Schwarz et al. 1998). For example, pumping tests conducted during the Vandenberg AFB demonstration project (Appendix A) underestimated flux significantly (roughly 50% of the actual flux), but it was later discovered that the flux estimates were so low because the pumping wells did not entirely capture the plume, which had been predicted from assumed K values. When more-accurate K values were used, the pumping tests were in fact both accurate and precise in their measurements of the plume area actually sampled. When important factors such as K are assumed, a sensitivity analysis should be performed and the results presented as a range.
One can reduce the error in pumping tests by stepping up the pumping rate over time. This technique has been recommended in a review of mass flux measurement methods (Goltz et al. 2007). The authors recommend starting at less than the suspected natural groundwater flow rate and monitoring the results at different steps until reaching a pumping rate that ensures complete capture without “overcapture” of the contaminated plume and potential error due to dilution by uncontaminated water. An abundance of data from well-spaced piezometers is very helpful in determining capture zones.
4.3 Passive Flux Meters
Recently, the PFM has been developed to measure cumulative groundwater and contaminant fluxes in the saturated zone at hazardous waste sites (Hatfield et al. 2002a, 2002b; Annable et al. 2005; Huluska et al. 2018). The PFM consists of a permeable sorbent infused with soluble tracers packed in a nylon mesh tube. The device is placed in a borehole or monitoring well for a known exposure period, where it intercepts the groundwater flow, causing dissolved contaminants to sorb to the sorbent and the soluble tracers to leach out. The measurements of the contaminants and the remaining resident tracer can then be used to estimate groundwater and contaminant fluxes. By using several PFMs across a transect, the average mass flux and total mass discharge through the control plane can be estimated.
All sorbents have a limited capacity to trap contaminants when used in a PFM. Using estimates of contaminant concentration and Darcy flux anticipated, the test duration can be selected to avoid loading the sorbent to capacity. In general, this is very unlikely for most organic contaminants on activated carbon. However, low molecular weight compounds should be checked carefully. If the compound mass on the sorbent is near the capacity, then some quantity of contaminant has passed through the device, and the mass flux reported should be noted as a minimum, recognizing that the actual mass flux was greater. For a more accurate value, the PFM should be redeployed for a shorter duration (M. D. Annable, personal communication, 2009).
The following section describes how the mass flux, Jc, is calculated based on the design and use of the PFM. The following equation from Hatfield et al. (2002b) can be used to determine the mass flux:

where
Jc = time-averaged advective contaminant mass flux, M/L2/t (e.g., mass/area/time)
CF = flux averaged concentration of contaminant in the groundwater, M/L3 (e.g., mass/volume)
q0 = specific discharge of the aquifer, L/t (e.g., length/time)
The PFM is designed with a diameter approximately the same as the diameter of the borehole or monitoring well in which it is installed to help ensure groundwater flow is through the PFM instead of around it in open space. The PFM may be separated into different vertical zones isolated by impermeable barriers such as rubber/neoprene washers. These help prevent vertical flow within the PFM (but not the filter pack) and allow the PFM to be used to assess different zones in the aquifer. PFM spacing should be based on the geology and groundwater flow characteristics of the aquifer (Annable et al. 2005).
When constructing the PFM, the sorbent, which can be varied based on the contaminant, is impregnated with a known amount of water-soluble tracers (Hatfield et al. 2004). The unit is then placed in a well or borehole and exposed to the groundwater flow for from a few days to a month. During the PFM deployment, portions of the soluble tracers are released, and contaminants are sorbed. The extent to which tracers are removed from and contaminants are loaded onto the PFM is determined by the groundwater velocity, the affinities of the tracers and contaminants to the PFM sorbent, and the concentrations of contaminants in the groundwater flowing through the PFM. The optimum exposure period would allow one half of the initial tracer mass to be removed from the PFM. When the PFM is removed, the sorbent is extracted to quantify the mass of contaminants intercepted by the groundwater flow and the mass of resident tracer remaining (MR) on the sorbent. If the MR value is >0.3, the following equation may be used to determine q, the specific discharge through the PFM assuming reversible, linear, and instantaneous contaminant partitioning between the sorbent and water (Annable et al. 2005):
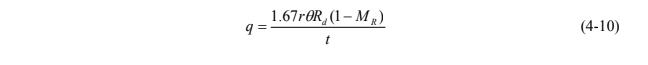
where
r = radius of the PFM cylinder, L (length)
θ = dimensionless water content of the PFM which may be determined by gravimetric analysis (only after conversion, must go from g water/g solid to volume of water/volume of soil or volume total)
Rd = retardation factor of the resident tracer on the sorbent (Note: The retardation factor in this equation assumes linear partitioning between the sorbent and the water.)
t = sampling duration
MR = relative mass of tracer remaining in the PFM sorbent (percentage)
For an equation applicable to MR values <0.3, see Annable et al. (2005). Since the flow is typically unknown in field applications, multiple tracers with differing retardation factors need to be applied to the sorbent. This method allows for flexibility when using different exposure periods for the PFMs.
The retardation factor of the resident tracer on the sorbent (Rd) is calculated by eq. 4-11 (Hatfield et al. 2004):
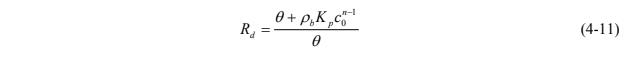
where
ρb = bulk density of the sorptive matrix, M/L3 (mass/volume)
c0 = initial dissolved aqueous resident tracer concentration in the pore fluid, M/L3 (e.g., mass/ volume)
KpE = Freundlich coefficient or the reversible distribution coefficient for the sorbent–aqueous phase partitioning of the resident tracer, L3n/Mn (volume/mass)
As the groundwater flows through the PFM, which is installed in a borehole or monitoring well, the fluid streamlines within the PFM are assumed to be parallel. This principle was demonstrated for a homogenous, permeable, circular element placed in a homogenous aquifer with a differing permeability (Strack and Haitjema 1981, Annable et al. 2005). Groundwater flow is assumed to be horizontal or near horizontal through the PFM (Hatfield et al. 2004). However, the permeability differences between the aquifer and the PFM may produce aquifer flows that converge or diverge near the PFM. This convergence or divergence (a ) must be taken into account when determining the undisturbed aquifer flow, q0. Since the specific discharge of water flowing through the sorbent in the PFM, q, is linearly related to the specific discharge of the groundwater (q0), the following equations show this relationship, where a is function of the difference in hydraulic conductivities between the aquifer and a monitoring well or borehole:
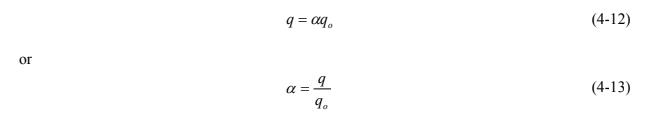
Specifically, for a PFM situated in a borehole, eq. 4-14 provides an estimation of a (Strack and Haitjema 1981):
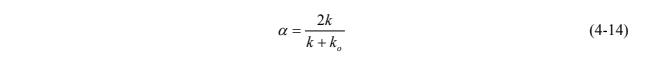
where
k = permeability of the PFM (darcies, or any unit consistent with ko)
ko = permeability in the immediate vicinity of the PFM in the formation (Note: This is needed even though tracers are used to estimate flow.)
For a fully screened monitoring well without a filter pack, a can be determined from eq. 4-15 (Hatfield et al. 2004):
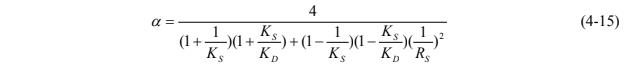
where
KD = KD/Ko , the dimensionless ratio of kD (the uniform hydraulic conductivity of the PFM sorptive matrix, L/t [length/time]) to ko (the uniform local hydraulic conductivity of the surrounding aquifer, L/t [length/time])
KS = Ks/Ko , the dimensionless ratio of ks (the well screen hydraulic conductivity) to ko (the uniform local hydraulic conductivity of the surrounding aquifer, L/t (length/time)
RS = ro/r , the dimensionless ratio ro (the outside radius of the well screen, L [length] to r (the PFM radius, L [length])
Using q = a × q0, the specific discharge of the aquifer, q0, may be determined. Next, the flux averaged concentration of the contaminant, CF, needs to be determined using eq. 4-16 (modified from Hatfield et al. 2004):
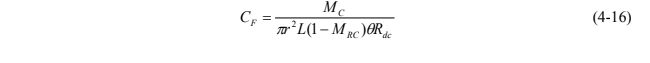
where
MC = mass of contaminant sorbed
L = length of the sorbent matrix for the vertical thickness of aquifer interval sampled
MRC = the relative mass of a resident tracer retained after time period t
r = radius of the PFM cylinder
Rdc = retardation of contaminant on the sorbent
θ = volumetric water content in the PFM
Subsequently, as further defined in Hatfield et al. (2004), the mass flux (Jc) may be calculated by multiplying the specific discharge of the aquifer (q0) by the flux averaged concentration (CF):

where
Jc = time-averaged advective contaminant mass flux, M/L2/t (e.g., mass/area/time)
CF = flux averaged concentration of contaminant in the groundwater, M/L3 (e.g., mass/volume)
q0 = specific discharge of the aquifer, L/t (e.g., length/time)
4.3.1 Simplified Method
This process of determining the mass flux can be simplified. If reversible, linear, and instantaneous contaminant partitioning between the water and sorbent is assumed, the contaminant mass flux (Jc) can be determined from eq. 4-18 (modified from Annable et al. 2005):
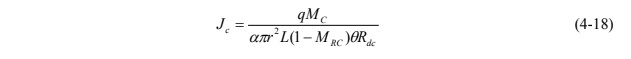
where
Mc = mass of contaminant sorbed
L = length of the sorbent matrix for the vertical thickness of aquifer interval sampled
Rdc = retardation of contaminant on the sorbent
MRC = the relative mass of a resident tracer retained after time period t where the tracer has the same retardation as Rdc
θ = dimensionless water content in the PFM
q = specific discharge of water through the PFM
r = radius of the PRM cylinder
a = convergence or divergence of flow around the PFM
This equation combines a few steps already discussed.
To determine the contaminant flux (Jc) for high values of Rdc or a short exposure period, the assumption can be made that all contaminant mass entering the monitoring well is adsorbed by the PFM sorbent. The following simplified equation (Annable et al. 2005) can then be used:
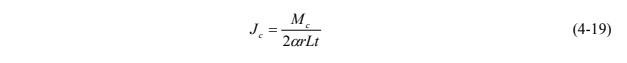
where
Mc = mass of contaminant sorbed
L = length of the sorbent matrix for the vertical thickness of aquifer interval sampled
r = radius of the PFM cylinder
t = exposure period of PFM to groundwater
a = convergence or divergence of flow around the PFM
A total time-averaged contaminant mass discharge Md (M/t) may be determined by spatially integrating the incremental measures of contaminant mass flux Jc (M/L2/t) and specific discharge q0 (L/t) across the control plane of area dA (L2) (modified from Hatfield et al. 2004).
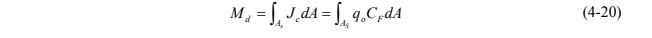
where
CF = flux averaged contaminant concentration in groundwater, M/L3 (e.g., mass/volume)
As = source area or the area of the control plane orthogonal to groundwater flow, L2
Similar to the transect method, the integration in eq. 4-21 can be approximated by summing sectionalized mass flux values across the control plan (Figure 2-3) where the sectionalized values can be obtained by interpolating the actual mass flux measurements from multiple locations. Any intepolation method can be used for this regionalization, and the results are subject to the benefits and limitations of the selected interpolation method. For example, the Theissen polygon method introduced in Step 4 of Section 4.1.1 can be used and the approximation equation as follows:
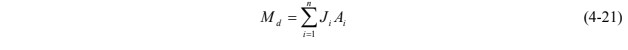
where
Md = mass discharge, M/t (mass/time)
Ji = mass flux estimate at location i, M/L2/t (mass/area/time)
Ai = area of polygon i, L2 (length2), the area that the mass flux estimate Ji represents
n = number of polygons sectionalizing the control plan
Although there are several technologies available to estimate mass flux, the PFM can directly measure subsurface solute flux at the monitoring locations in the plume, which the transect method alone cannot, and can provide a simultaneous measure of both cumulative groundwater and contaminant fluxes. The PFM is able to show variations in groundwater and contaminant fluxes over the depth of an aquifer, which contributes to better spatial interpretation and subsequently better site characterization.
4.3.2 Sensitivity/Uncertainty
The PFM is a developing technology which provides mass flux data similar to data collected by other sampling methods under specific conditions. For example, the PFM test methods have been compared to other mass discharge measurement methods at two sites (Brooks et al. 2008):
- Hill AFB
- pretreatment—PFM: 76 g/d, TM: 78 g/d
- post-treatment—PFM: 6 g/d, TM: 7.2 g/d
- Ft. Lewis
- pretreatment—PFM: 646 g/d, TM: 599 g/d
- post-treatment—PFM: 2.3 g/d, TM: 1.9 g/d
Section 4.2.5 has a description of both sites. Variation 3 was used to compute the mass discharge for the transect method. The absolute accuracy of either method is not known. The relative differences between the two methods ranged from –17% to –8% as determined by subtracting the PFM measurements from the TM measurements and dividing by the TM measurements. The differences are relatively small considering the variability in groundwater flow and groundwater monitoring data and the overall range in mass discharge estimates, which has a factor of 200 or more.
However, there are several uncertainties associated with the PFM technology:
- Biostimulation conducted at National Aeronautics and Space Administration (NASA) Launch Complex (LC)-34 site appeared to influence the mass flux calculations (ESTCP 2006b). The integrity of the tracer alcohols appeared to be compromised during biostimulation and bioaugmentation, which subsequently overestimated water flux. This result was demonstrated as initial estimate of groundwater flux estimates made by the PFMs and multilevel samplers (MLSs) were within 20% when using ethanol as a tracer. During biostimulation, the isopropanol tracer provided an estimate within 30%. After bioaugmentation, estimates were within 67%. Also during bioremediation, when comparing the estimates of contaminant fluxes using the PFMs and the transect method, the estimates were significantly different (95%–189%). PFM estimates for vinyl chloride and ethene fluxes were much higher than estimates using the transect method or extraction well data. This suggests that the PFM sorbent trapped volatile compounds or that TCE and DCE degraded while on the sorbent (Baumann 1989, Scamehorn 1979, ESTCP 2006b.)
- At the second site (Port Hueneme, see Appendix B), the authors noted that PFMs installed in pushed wells tended to calculate a lower groundwater and contaminant flux than those installed in drilled wells. This was also observed by Bartlett et al. (2004) and ESTCP (2006c). However, the flux-averaged concentrations (CF) between the drilled and pushed wells did not vary significantly. This observation may be related to convergence or decreased hydraulic conductivity associated with the pushed wells.
- The PFM technique appears better suited to quantify mass discharge in a permeable unconsolidated aquifer. A new type of PFM device for fractured-rock applications is being developed under ESTCP (Dougherty et al. 2018.). Site characterization requires a detailed understanding of the geology to understand how best to construct and place the PFMs.
- The PFM records a point measurement over time and therefore does not account for contaminants in flow paths not intercepted by the flow meter. As with all of these methods, the PFM assumes horizontal flow, which may not be valid at all sites. The authors’ experience is that vertical flow occurs at most sites but is generally small compared to the horizontal flow. However, there are certainly cases where vertical gradients are important or even dominate. In these cases mass flux/discharge measurement techniques should be evaluated carefully to determine whether the vertical flow will cause faulty results.
Hatfield et al. (2004) reported that the use of PFMs in the field poses several challenges. First, multiple wells and PFMs are needed to estimate total contaminant discharge through the transect. The resultant discharge estimate is sure to contain uncertainties, as it is generated from spatially integrating point measures of flux. Second, competitive sorption or rate-limited sorption may limit the ability of the PFM to capture and retain target contaminants. If either is not considered in the interpretation of results, calculations may not reflect true contaminant fluxes. Finally, long-term flux monitoring may be problematic because natural changes in flow direction can invalidate flux measurements. PFMs should not be applied in wells that contain NAPLs, as shown by a technology evaluation study performed at one site.
4.4 Transects Based on Isocontours
At some sites, direct mass flux estimates are not available by any of the methods described in the previous section. In that case, data from existing monitoring well networks can be used to develop mass flux estimates (Nichols and Roth 2004). In this case, monitoring points that are not located in a transect are used to construct a contour map of groundwater concentrations, either by hand or by using computer contouring tools supervised by knowledgeable groundwater personnel. The key point behind the isocontour-based transect approach is that the resulting contour lines represent the hydrogeologist’s best estimate of the distribution of concentration in a plume. If there are a sufficient number of monitoring points and if the hydrogeologist’s contouring is accurate, the resulting isocontour-based transects would be similar to an actual transect constructed in the field. If there is reason to doubt the accuracy of the contour lines due to a limited number of monitoring well points, then the resulting mass flux estimates will have higher uncertainty. In other words, if a groundwater contour map is accurate enough to be used for regulatory and/or design purposes, then it is likely that there is useful information that can be converted to mass flux and mass discharge estimates.
Figures 4-11 and 4-12 show an example of this method for a single-level monitoring system. In this example, the general method is the same as that described in Section 4.1.1 but with the measurement points being the intersection of contour lines and the isocontour-based transect rather than an actual monitoring point. In this case the width of each polygon is the distance between contour lines on a transect, and the depth is the saturated thickness of the aquifer.
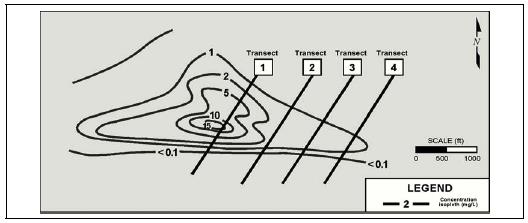
Figure 4-11. Example transects, Dover AFB, Delaware. (Adapted from Einarson 2001.)
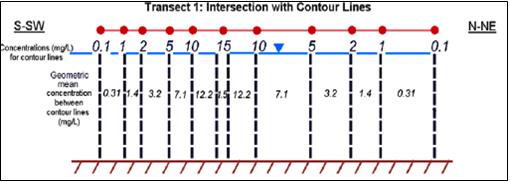
Figure 4-12. Example two-dimensional transect based on isocontour data.
This method may have more uncertainty than high-density multilevel transect data. Care must be taken using this method as contours prepared by either hand or computer that do not sufficiently consider the site-specific geology and controlling preferential pathways often seen in contaminant transport may be misleading. The contours must also take into account vertical variations in flow and transport pathways and distribution. However, useful mass flux estimates may be generated if the monitoring well network is sufficiently dense. The method will be more accurate when the screened interval of the wells in the monitoring network intercepts all or a large fraction of the contaminated plume thickness and when the sample that is collected represents a flow-weighted average concentration. For the last condition, low-flow sampling may not yield a flow-weighted average concentration if the sample is not collecting water from the entire screened interval. Long-screened wells are proposed by some researchers as an inexpensive tool to provide mass discharge data because multiple vertical samples are not needed; rather, the well will represent the flow-weighted concentration of the plume at this location. This method will provide mass discharge information but does not provide any information on the likely maximum concentration at that monitoring point due to the vertical averaging.
4.5 Solute Transport Models
Several solute transport models have dedicated routines to calculate mass flux from the model input data (Nichols and Roth 2004; Farhat, Newell, and Nichols 2006; see Table 4-3). These models require that both groundwater flow data and contaminant data be entered into the model where it is processed to generate output, typically in the form of groundwater concentrations. However, since both flow and concentration data are used in the model, mass flux data can often be obtained from the application of a solute transport model.
Table 4-3. Solute transport models used for mass flux estimates
| Model | Application and type | Type of mass flux output | Source |
| BIOSCREEN | Fuel hydrocarbon MNA Analytical | Calculated from a 5 × 11 array of concentration values | https://www.epa.gov/water-research/bioscreen-natural-attenuation-decision-support-system |
| BIOCHLOR | Chlorinated solvent MNA Analytical | Calculated from a 5 × 10 array of concentration values | https://www.epa.gov/water-research/biochlor-natural-attenuation-decision-support-system |
| BIOBALANCE | Chlorinated solvent MNA Analytical | Calculated from a 30 × 30 array of concentration values | https://www.gsi-net.com/en/software/free-software.html |
| MODFLOW/MT3DMS | General Numerical | Calculated at source/sink objects | https://www.usgs.gov/mission-areas/water-resources/science/modflow-and-related-programs?qt-science_center_objects=0#qt-science_center_objects |
| MODFLOW/RT3DMS | General, sequential degradation Numerical | Calculated at any transect in model using the rtFlux module | https://www.pnnl.gov/projects/multi-species-reactive-transport-simulation-software-groundwater-systems |
| MODFLOW/MT3D | General Numerical | Can be calculated externally in spreadsheets using ZoneBudget routine for flow and concentration output | https://www.usgs.gov/mission-areas/water-resources/science/modflow-and-related-programs?qt-science_center_objects=0#qt-science_center_objects |
| MODFLOW/MT3D | General Numerical | The TOBS Package can calculate the (total) mass flux for selected individual objects such as a section of a river | https://www.usgs.gov/mission-areas/water-resources/science/modflow-and-related-programs?qt-science_center_objects=0#qt-science_center_objects |
| REMChlor-MD | Hydrocarbon, chlorinated solvent | Calculated using analytical model | https://www.epa.gov/water-research/remediation-evaluation-model-chlorinated-solvents-remchlor |
Examples of this approach in the literature include the following:
- Clausen et al. (2003) used “MODFLOW coupled with MT3D to conduct a transport simulation. Mass was added to the model at the source until a reasonable match was obtained between the model simulated groundwater plume and the actual plume. Once this was achieved, the model was used to determine the flux rate of RDX to groundwater, which turned out to be approximately 0.1 kg/year.”
- Christensen, Korsgaard, and Riss (2002) used a transient unsaturated zone model to estimate a mass flux of 0.15 kg/year of PCE to groundwater.
- Thuma, Kremesec, and Kolhatkar (2001) used MODFLOW and MT3D to simulate an MtBE plume in Long Island and calculated mass discharge, which was called “mass flux” in their paper, at three locations. The modeled mass discharge near the source zone (310 g/d) was similar to the mass discharge measured via the transect method (250 g/d). Larger differences between the mass discharge generated by the model and the transect method occur because the model may not have captured degradation of MtBE in the downgradient portion of the plume.
- Eberts et al. (2005) used the BIOCHLOR model at a phytoremediation site in Texas to estimate total mass changes over distance. The model indicated that there was a 44% decrease in mass discharge of TCE, referred to in this paper as “mass flux,” partially due to biodegradation related to cottonwood trees.
- Johnson, Truex, and Clement (2006) reported on the use of the rtFlux module in RT3D at a site where mass discharge rates of 160,000 g/d for a no-pumping case and ~8 g/d for a case where pump and treat was used to hydraulically contain a large plume.
- The MODFLOW/MT3D model was applied to a large, multisource industrial site in the Midwest and provided an estimate that ~50,000 g/d of mass discharge of chlorinated compounds would occur without the presence of groundwater containment system. A containment system was predicted to reduce this mass discharge by over 90%.
4.6 Key Considerations Using Models to Obtain Mass Flux
The different types of models are based on different assumptions and calculation techniques. Analytical models make use of simplifying assumptions such as uniform one-dimensional flow fields, simple source characteristics, and other factors that make these models useful for screening or planning purposes. As would be expected, the mass flux estimates from an analytical model also would be better suited for screening or planning purposes as opposed to the case where very detailed mass flux data are required to ensure the reliability of some type of remedial design at large or very complex sites. The accuracy of mass flux data from numerical models would, as expected, be very dependent on the accuracy of the input data for flow and contaminant concentration and mass.
The amount of data available to input into the model is also significant. If there are not enough data to generate node sizes appropriate to the local geology and hydrogeology, the model may oversimplify site conditions. Care must also be taken during model uncertainty assessment and calibration to ensure site conditions are accurately represented.
One study of an MtBE plume on Long Island (Thuma, Kremesec, Kolhatkar 2001) compared the MtBE mass discharge using the transect method to the mass discharged derived from a groundwater solute transport model. The results were similar: 250 g/d for the transect method and 310 g/d for the model (24% relative difference). As mass discharge measurements between sites can vary over many orders of magnitude, these two values (250 and 310 g/d) are very close.
4.7 General Comparison of Five Mass Flux Measurement Methods
A qualitative comparison of five mass flux measurement methods was developed by Goltz et al. (2007) and is presented in Table 4.4. The five methods were as follows:
- transect method (TM)
- passive flux meter (PFM)
- integral pump test (IPT) (The original paper referred to this as integral groundwater investigation method.)
- modified integral pumping test (MIPT) (The original paper referred to this as integral pump test method, or IPT)
- tandem circulation wells (TCW) (The original paper referred to this as tandem recirculation wells, or TRW)
Table 4-4. Comparison of groundwater contaminant flux measurement methods
(Modified from Goltz et al. 2007.)
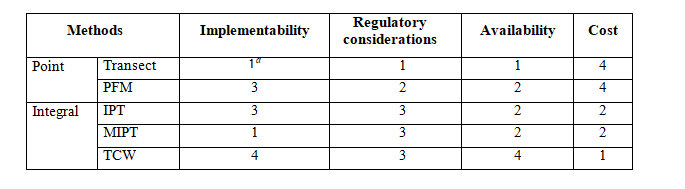
Four metrics were evaluated: implementability, regulatory, availability, and cost. No site-specific limitations for any specific method were provided by the authors, suggesting that each method is applicable to a wide range of contaminants and hydrogeologic settings. Additional comments regarding how these methods compared are reproduced below (Goltz et al. 2007):
Implementability. This is a measure of how straightforward and simple application of each method would be. The conventional transect method, which consists of installing monitoring wells in order to measure the hydraulic gradient and contaminant concentrations, as well as conducting a pumping test to estimate hydraulic conductivity, is simple to implement. All steps in applying the method are commonly applied in the field and well understood. The MIPT method is equally straightforward, requiring installation of standard pumping and monitoring wells. The PFM, IPT, and TCW methods are somewhat more complex. The PFM method requires quantification of the contaminant which is sorbed onto the sorbent, as well as measurement of the loss of resident tracer. Also, data interpretation requires estimation of the aquifer area associated with each PFM. These measurements require special expertise. The IPT requires interpretation of the (concentration vs. time) data, which is somewhat complex (Bockelmann, Ptak, and Teutsch 2001; Zeru and Schäfer 2005). To implement the TCW method requires construction of special dual-screened wells. The downflow well in particular requires special construction in order to pump water downwards. Also, data interpretation requires somewhat complicated inverse modeling techniques.
Regulatory. Both the TCW and PFM methods involve injecting tracers into the aquifer, and this may raise some regulatory concerns. In addition, the TCW method involves circulating contaminated groundwater in the subsurface. If contaminant concentrations vary in space (particularly vertically), this may also concern regulators. The IPT and MIPT methods are of concern since they require contaminated groundwater extraction. The conventional transect method poses the least regulatory concern.
Availability. The transect approach is well understood, has appeared many times in the literature, and involves no special expertise to implement. Therefore, it is readily available from most purveyors of groundwater remediation services. The other methods are all in some stage of technology transfer, with the PFM and IPT methods furthest along, followed by the MIPT and TCW methods. The PFM and IPT methods are well documented in the peer-reviewed literature and could probably be applied by well-trained practitioners who are familiar with the literature. Although the IPT method is new and the method has yet to be documented in the literature, the steps in implementing the method are conventional. Currently, the TCW method is unavailable for field application. The method has yet to appear in the peer-reviewed literature, and implementation would require the assistance of the technology developers.
Cost. It is difficult to quantify the cost and the cost/benefit of acquiring detailed mass flux information. It is generally perceived that knowing the mass flux would help regulators and consultant, but it is difficult to quantify these perceived benefits. As more case studies become available, this information may be forthcoming. Please see Kram et al. (2008) for additional information on cost and performance of HRP coupled to the GeoVIS.
Though mass flux is a well-established concept, interest in its use has increased considerably because recent developments have made mass flux estimates more useful and cost-effective (Ptak, Schwarz, and Teutsch 1998; Hatfield et al. 2002a, 2002b). When used in conjunction with traditional techniques that are commonly required by regulatory agencies (e.g., point estimates of concentration, etc.), there may be considerable benefits to be gained by implementing an assessment and remediation plan that includes a flux characterization component. These may include the following:
- reduce the volume of the treatment zone by providing evidence of the high-flux tubes, thereby allowing targeted treatment
- improve the understanding of appropriate active remediation contaminant levels that may and must be achieved by allowing better validation of the natural attenuation capacity of the aquifer system
- improve the estimation of the treatment duration by examining mass flux as a function of time along a downgradient plane
Goltz et al. (2007) did not evaluate one frequently used method, mass discharge estimation using transects based on isocontours (Section 4.4), in their comparison of different mass discharge methodologies. This method has the advantage of being very inexpensive, as most site assessment programs result in isocontour maps of concentration. For certain questions (such as a screening analysis to estimate plume strength), mass discharge estimation using transects based on isocontours is perceived by some practitioners to be a very cost-effective way to obtain useful site data.
4.8 Managing Uncertainty
As has been discussed in previous sections, mass flux and mass discharge estimates can be applied in several phases of the site investigation and remediation process. These estimates, while very useful, are also characterized by significant uncertainty due to the method by which they are developed (Section 2.5). The challenge then is to determine the acceptable level of uncertainty for the intended application of mass flux or discharge estimates and how to manage that uncertainty. While what is “acceptable” will be driven by site- and project-specific factors, such as carcinogenicity of the COC and the proximity and sensitivity of potential receptors, there are general constraints in managing or reducing downside risks of uncertainty:
- Level of available funding—Increased sample collection and infrastructure increase capital and labor costs.
- How the flux estimates will be used—Monitoring natural attenuation processes may tolerate more uncertainty than demonstrating compliance.
- Phase of the project—More accurate data may be more useful during certain task or project phases, justifying more sampling and infrastructure installation.
- Project participants’ experience with and confidence in mass flux estimates.
Mass discharge can have a wide range when comparing source strength for different sites. For example, the case studies listed in Appendix A have a range of eight orders of magnitude for mass discharge (0.00078–160,000 g/d) measured at various sites. This is not unexpected because hydraulic conductivity values can range over six or seven orders of magnitude and concentrations can also span a similar range. Therefore, the accuracy of mass flux estimating methods should be considered in this context. In other words, mass flux or mass discharge estimates with uncertainty of an even order of magnitude (factor of 10) can still provide useful information for site management. The data quality objectives related to the use of a mass flux or mass discharge estimate should be determined to ensure that an appropriate method with sufficient data density is used for their development. For example, detailed design projects need more-refined mass flux/discharge estimates, while screening level studies can be successful despite higher uncertainty in the mass flux/discharge estimates.
In highly heterogeneous environments, it may not be cost-effective, or even physically possible, to collect enough samples to obtain a sound estimate using conventional statistical methods. Research is needed to develop statistical approaches that allow for cost-effective determination of integrated mass flux in natural aquifers.
Click Here to download the entire document.